Applications of Newton's Laws of Motion
Applications of Newton's Laws of Motion: Overview
This topic consists of various concepts like Free Body Diagram,Motion of Connected Bodies,Motion on Inclined Plane, etc.
Important Questions on Applications of Newton's Laws of Motion
A block of mass m is placed on a smooth wedge of inclination The whole system is accelerated horizontally so that the block does not slip on the wedge. The force exerted by the wedge on the block (g is acceleration due to gravity) will be
The coefficient of static friction, , between block of mass and the table as shown in the figure is . What would be the maximum mass value of block so that, the two blocks do not move? The string and the pulley are assumed to be smooth and massless .
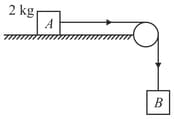
A monkey of mass is holding a vertical rope. The rope will not break when a mass of is suspended from it, but will break if the mass exceeds . What is the maximum acceleration with which the monkey can climb up along the rope?
A block has been placed on an inclined plane with the slope angle block slides down the plane at constant speed. The coefficient of kinetic friction is equal to :
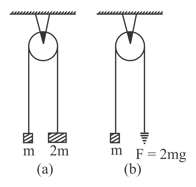
The pulley arrangements of the figure. (a) and (b) are identical. The mass of the rope is negligible. In (a) the mass is lifted up by attaching a mass to the other end of the rope. In (b), is lifted up by pulling the other end of the rope with a constant downward force . The acceleration of in both cases is?
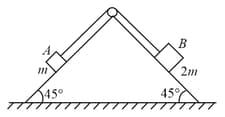
Block of mass and block of mass are placed on a fixed triangular wedge by means of a massless inextensible string and a frictionless pulley as shown in figure. The wedge is inclined at to the horizontal on both sides. The coefficient of friction between block and the wedge is and that between block and the wedge is . If the system of and is released from rest, find the magnitude and direction of the force of friction acting on
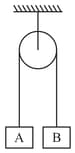
A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is , then the ratio of the masses is –
Two masses and tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when left free to move? ( )
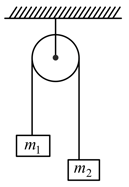
Two masses and tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when left free to move? ( )
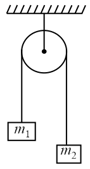
A spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads when the lift is stationary. If the lift moves downward with an acceleration of , the reading of the spring balance will be,
A particle starts sliding down a frictionless inclined plane. If is the distance travelled by it from time to , the ratio is
Two blocks of mass andare arranged as shown and released from rest. Assuming string and pulley to be ideal, find the separation between them after []
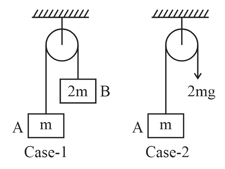
If acceleration of block in case is and in case is , then is
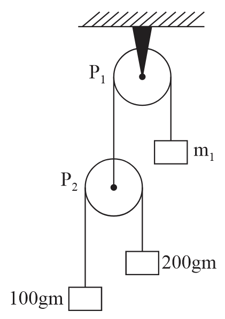
In the system of pulleys shown what should be the value of such that remains at rest: (Take )
A block of mass starting from rest pulled up on a smooth incline plane making an angle of with horizontal with an effective acceleration of . The power delivered by the puling force at from the start is _____ .
[Use ]
(Calculate the nearest integer value)
As per given figure, a weightless pulley P is attached on a double inclined frictionless surfaces. The tension in the string (massless) will be (if )
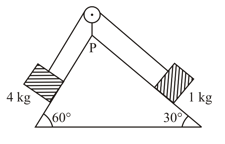
Two masses and are connected by a mass less string which passes over a light frictionless pulley shown in the figure. The masses are initially held with equal lengths of the strings on either side of the pulley. Find the velocity of the masses at the instant the lighter mass moves up a distance of. This string is suddenly cut at that instant. Calculate the time taken by each mass to reach the ground. Take .
A body of mass slides down with an acceleration of on a rough inclined plane having a slope of . The external force required to take the same body up the plane with the same acceleration will be ()
The ratio of time period of oscillation of block in figure and figure is
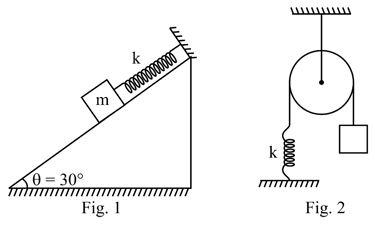
Note:All the pulleys are ideal.
A box of mass is pushed up an inclined plane from rest with a force of . The plane makes an angle of with the horizontal. The coefficient of kinetic friction between the plane and the box is . Using work-energy theorem, calculate the speed of the box after it has been pushed for . Take
